数据结构与算法开篇

算法

先来看一道题:

如果 a+b+c=1000，且 a^2+b^2=c^2（a,b,c 为自然数），如何求出所有a、b、c可能的组合?

  1. 枚举法

a = 0

b = 0

c = 0 -> 1000

控制两个变量不变，一个变量变，c变到1000后结束循环，a = 1， b=0, c = 0 -> 1000，不断去枚举求出所有的值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# encoding=utf-8
import time

start_time = time.time()
for a in range(0, 1001):
    for b in range(0, 1001):
        for c in range(0, 1001):
            if (a+b+c == 1000) and (a**2+b**2 == c**2):
                print(f"a:{a}, b:{b}, c:{c}")
end_time = time.time()
print(f"cost {end_time-start_time} s")
print("finished")

# output
a:0, b:500, c:500
a:200, b:375, c:425
a:375, b:200, c:425
a:500, b:0, c:500
cost 100.20555758476257 s
finished
Process finished with exit code 0
  1. 对算法进行优化
1
已知 a + b + c = 1000, 则可使 c = 1000 - (a+b), 使得算法时间复杂度从 O(n^3) --> O(n^2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
for a in range(0, 1001):
    for b in range(0, 1001):
        c = 1000 - (a+b)
        if (a + b + c == 1000) and (a ** 2 + b ** 2 == c ** 2):
            print(f"a:{a}, b:{b}, c:{c}")
            
# output
a:0, b:500, c:500
a:200, b:375, c:425
a:375, b:200, c:425
a:500, b:0, c:500
cost 0.7595357894897461 s
finished

Process finished with exit code 0

说明解决同一个问题有多个算法，不同算法之间效率有所差异。

算法效率衡量

单靠时间可靠吗？

不同机器不同环境的运行时间是不一样的，所以单靠时间是不准确的。

每台机器执行的总时间不同，但每一台机器执行的基本运算数量大体相同，可以直接用基本运算步数来衡量算法的优劣。

T(n)的渐近时间复杂度是O(n)，一般用O来表示算法时间复杂度。

时间复杂度的几条基本计算规则

  1. 基本操作，即只有常数项，认为其时间复杂度为O(1)
  2. 顺序结构，时间复杂度按加法进行计算
  3. 循环结构，时间复杂度按乘法进行计算
  4. 分支结构，时间复杂度取最大值
  5. 判断一个算法的效率时，往往只需要关注操作数量的最高次项，其它次要项和常数项可以忽略
  6. 在没有特殊说明时，我们所分析的算法的时间复杂度都是指最坏时间复杂度

常见的时间复杂度

执行次数函数举例 阶 非正式术语
12 O(1) 常数阶
2n+3 O(n) 线性阶
3n2+2n+1 O(n2) 平方阶
5log2n+20 O(logn) 对数阶
2n+3nlog2n+19 O(nlogn) nlogn阶
6n3+2n2+3n+4 O(n3) 立方阶
2^n O(2^n) 指数阶

注意，经常将log2n（以2为底的对数）简写成logn

常见时间复杂度之间的关系

算法效率关系

所消耗的时间从小到大

Python内置类型性能分析

timeit模块

timeit模块可以用来测试一小段Python代码的执行速度。

class timeit.Timer(stmt=’pass’, setup=’pass’, timer=)

Timer是测量小段代码执行速度的类。

stmt参数是要测试的代码语句（statment）；

setup参数是运行代码时需要的设置；

timer参数是一个定时器函数，与平台有关。

timeit.Timer.timeit(number=1000000)

Timer类中测试语句执行速度的对象方法。number参数是测试代码时的测试次数，默认为1000000次。方法返回执行代码的平均耗时，一个float类型的秒数。

list的操作测试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def test1():
   l = []
   for i in range(1000):
      l = l + [i]
def test2():
   l = []
   for i in range(1000):
      l.append(i)
def test3():
   l = [i for i in range(1000)]
def test4():
   l = list(range(1000))

from timeit import Timer

t1 = Timer("test1()", "from __main__ import test1")
print("concat ",t1.timeit(number=1000), "seconds")
t2 = Timer("test2()", "from __main__ import test2")
print("append ",t2.timeit(number=1000), "seconds")
t3 = Timer("test3()", "from __main__ import test3")
print("comprehension ",t3.timeit(number=1000), "seconds")
t4 = Timer("test4()", "from __main__ import test4")
print("list range ",t4.timeit(number=1000), "seconds")

# ('concat ', 1.7890608310699463, 'seconds')
# ('append ', 0.13796091079711914, 'seconds')
# ('comprehension ', 0.05671119689941406, 'seconds')
# ('list range ', 0.014147043228149414, 'seconds')

另外，“l += [i]”操作的执行效率要高于“ l = l + [i]” ，因为python对“+=”操作做了个优化。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# list的操作测试
def test1():
    l = []
    for i in range(1000):
        l = l + [i]

def test2():
    l = []
    for i in range(1000):
        l += [i]

def test3():
    l = []
    for i in range(1000):
        l.extend([i])

import timeit

t1 = timeit.Timer("test1()", "from __main__ import test1")
print("l = l + [i] ", t1.timeit(number=1000), "seconds")
t2 = timeit.Timer("test2()", "from __main__ import test2")
print("l += [i]", t2.timeit(number=1000), "seconds")
t3 = timeit.Timer("test3()", "from __main__ import test3")
print("l.extend([i])", t3.timeit(number=1000), "seconds")

# output
l = l + [i]  0.88471 seconds
l += [i] 0.05781510000000001 seconds
l.extend([i]) 0.06964039999999994 seconds

Process finished with exit code 0

pop操作测试

1
2
3
4
5
6
7
8
9
x = range(2000000)
pop_zero = Timer("x.pop(0)","from __main__ import x")
print("pop_zero ",pop_zero.timeit(number=1000), "seconds")
x = range(2000000)
pop_end = Timer("x.pop()","from __main__ import x")
print("pop_end ",pop_end.timeit(number=1000), "seconds")

# ('pop_zero ', 1.9101738929748535, 'seconds')
# ('pop_end ', 0.00023603439331054688, 'seconds')

测试pop操作：从结果可以看出，pop最后一个元素的效率远远高于pop第一个元素

可以自行尝试下list的append(value)和insert(0,value),即一个后面插入和一个前面插入？？？

list内置操作的时间复杂度(考虑最坏时间复杂度)

list操作

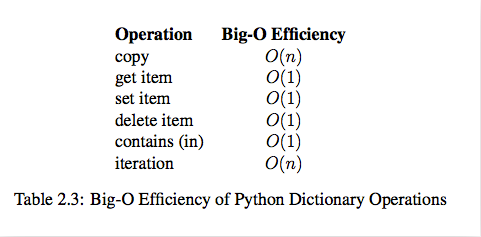
dict内置操作的时间复杂度

dict操作

数据结构

先来看一道题:

如果要存储一个班级学生的name、age、hometown，采取什么结构保存?

list(列表)、dict(字典)、set(集合)、tuple(元组)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 1.stus
[
    ("zhangsan", "18", "BeiJing"),
    ("zhangsan", "18", "BeiJing"),
    ("zhangsan", "18", "BeiJing"),
] 
# 2.stus
[
    {
        "name":"zhangsan",
        "age":"18",
        "hometown":"BeiJing"
    }
]
# 3.stus
{
    "zhangsan":{
        "age":"18",
        "hometown":"BeiJing"
    }
}

# 查找某一个学生的年龄家乡所需时间复杂度：
# 1.O(n)
# 2.O(n)
# 3.O(1)

概念

数据是一个抽象的概念，将其进行分类后得到程序设计语言中的基本类型。如：int，float，char等。数据元素之间不是独立的，存在特定的关系，这些关系便是结构。数据结构指数据对象中数据元素之间的关系。

Python给我们提供了很多现成的数据结构类型，这些系统自己定义好的，不需要我们自己去定义的数据结构叫做Python的内置数据结构，比如列表、元组、字典。而有些数据组织方式，Python系统里面没有直接定义，需要我们自己去定义实现这些数据的组织方式，这些数据组织方式称之为Python的扩展数据结构，比如栈，队列等。

算法与数据结构的区别

数据结构只是静态的描述了数据元素之间的关系。

高效的程序需要在数据结构的基础上设计和选择算法。

程序 = 数据结构 + 算法

总结：算法是为了解决实际问题而设计的，数据结构是算法需要处理的问题载体

抽象数据类型(Abstract Data Type)

抽象数据类型(ADT)的含义是指一个数学模型以及定义在此数学模型上的一组操作。即把数据类型和数据类型上的运算捆在一起，进行封装。引入抽象数据类型的目的是把数据类型的表示和数据类型上运算的实现与这些数据类型和运算在程序中的引用隔开，使它们相互独立。

最常用的数据运算有五种：

  • 插入
  • 删除
  • 修改
  • 查找
  • 排序

一个Stus的抽象数据类型代码：

1
2
3
4
5
class Stus(object):
    def adds(self):
    def pop(self):
    def sort(self):
    def modify(self):

书籍推荐

Python

算法导论

数据结构与算法C语言描述